[ARCHIVED] How would you handle a formula question with multiple answers?

[lph]

Is there a way to handle a formula question with multiple answers?

For example, a ball is tossed up and the student is asked to calculate the time when the ball is in a particular position. This is solved through a quadratic equation and there are two answers: the time up and the time down.

In this case, the question could be rearranged to ask what is the time up OR what is the time down? However, what if the question couldn't be rearranged. What are the options? How are teachers getting around this situation? Are teachers rewriting the question or is there an approach being used that someone is will to share?

[James]

lph, 

Currently, the only way I can think of to handle this is to be specific in your question. We do this with spring problems in differential equations.

What is the first time the object passes through the position 10 cm?

What is the first time the object passes through the position 10 cm on its way downward?

If the question cannot be rearranged, then you still have to rearrange the question because Canvas doesn't support multiple answers.

What is the lesser of the two values?

What is the greater of the two values?

You could ask for a non-answer.

What is the product of the two answers?

What is the sum of the two answers?

Those aren't always good, because if you know the shortcut you don't actually have to work out the answers. In ax²+bx+c=0, the product is c/a and the sum is -b/a.

I have gotten fancy with the question itself sometimes and used an if() function to determine the correct answer. I'm writing this using Classic Quizzes notation.

When you preview it, you get

There's probably a clearer way to word the statement about which answer to give, I've just demonstrating what can be done.

[lph]

As always, it took time to digest everything you were suggesting. 

This was the latest attempt to have the question specify the up or the down time. There couldn't be any cross over between the v and y variables or else the formula ended up producing imaginary numbers. 

What do you think of the attempt at the formula? It's my attempt at the quadratic formula to solve for the time. 

Next, will be an attempt to use the IF as you describe. Crossing fingers !

[James]

lph, your login changed on me and it took a second to figure out who LPH was.

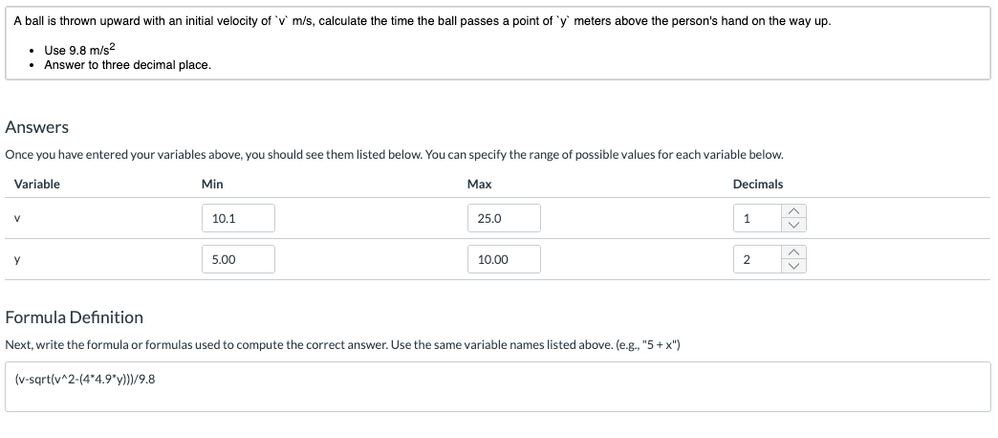
We normally take g=-9.8m/s/s rather than +9.8. Gravity acts down, you're throwing the ball up.

That makes the equation: -4.9t^2+vt=y or -4.9t^2+vt-y=0 or 4.9t^2-vt+y=0.

a=4.9, b=-v, and c=y

t1=(v-√(v²-19.6y))/9.8

t2=(v+√(v²-19.6y))/9.8

You want the time on the way up, which would be the first time, so it looks like you have it.

As for the range settings on the random variables, there is a problem.

You need the discriminant b^2-4ac > 0 in order to have two distinct real roots.

That's v²-19.6y > 0 or y < v²/19.6

That means that you are likely to get imaginary roots with your settings. For example, if v=10.1 and y=10, then v²-19.6y=-94ish

That is, the v=10 only guarantees a root when y=5. If y > 5.1 when v = 10, then there is no real answer to your question.

If you restrict 5<y<10, then you should make sure that v> √(19.6y). That gives you 9.9<v<14, so you would need to make sure that v>14 to guarantee real roots. The upper bound is up to you, it's the lower bound you need to be careful with.

If you restrict 5<y<8, then 9.8<v<12.5, so pick v>12.5.

Note I'm using strict inequalities here, when I say v>12.5, I mean start it at 12.6 or more -- 13 would be better.

If you're only going to ask one question, you could put it in a bank and randomly pick whether the person got the way up or the way down. That would be a lot simpler than using the IF().