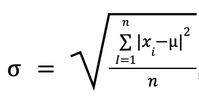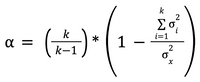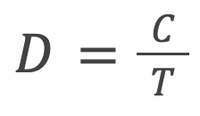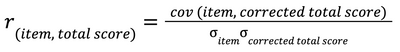The Quiz and Item Analysis report is a request-based report. The report includes responses received up until the point of report creation. However, the following submissions are not included in the Quiz and Item Analysis report:
- Submissions that have not yet been evaluated by the auto-grader
- Multiple attempts for quizzes
- Note: Only the last attempt for a quiz is included in the report
- Questions which have not been graded for at least half of the submissions
- Notes:
- The remainder of the questions are filtered again to exclude submissions with ungraded questions
- Maximum possible points for the quiz is reduced to match the number of points for the questions included in the report
- Submissions added by an instructor when previewing a quiz or in Student view
Quiz and Item Analysis Report Rules
Report data may display differently due to the following rules:
- In certain scenarios, some metrics cannot be calculated based on the available input. In these cases, metrics display “N/A” (Not Applicable) instead of the value. For instance, if all questions are randomized items in a quiz, Cronbach’s Alpha cannot be calculated. Similarly, if segmenting the students into 3 groups is not feasible, the discrimination index cannot be calculated.
- Percentage-based metrics are rounded to the closest integer, while other metrics are rounded to two decimal places.
Quiz Summary
This section defines the data points that can be found in the Quiz Summary section of the report.
High Score
Displays the highest percentage score awarded among students who took the quiz.
Low Score
Displays the lowest percentage score awarded among students who took the quiz.
Mean Score
Displays the average percentage score among students who took the quiz.
Median Score
Displays the middle value of percentage scores among the students who took the quiz when all the scores are arranged in ascending order. Unlike the mean score, which can be influenced by extreme values, the median is not affected by outliers.
Mean Elapsed Time
Displays the average time taken to complete the quiz.
Score Distribution Chart
Displays a distribution of percentage scores achieved among students who took the quiz.
Standard Deviation
What is Standard Deviation?
Standard deviation is a measure of the average absolute deviation of scores around the mean. A low standard deviation indicates, on average, the scores tend to be close to the mean of the set. A high value indicates, on average, scores vary widely from the mean of the data set. Standard deviation’s unit of measurement should be the same as the displayed mean. For example if a mean is listed as a percentage value, the standard deviation should also be listed as a percentage value.
How is the Standard Deviation calculated?
Standard Deviation is calculated by finding the square root of the average of the squared differences between each submission and the mean:
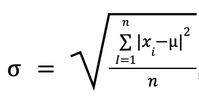 Standard Deviation Formula
Standard Deviation Formula
where 𝑛 is the number of responses, 𝜇 is the mean score, and 𝑥ᵢ is the percentage score of the i-th submission.
How do outliers affect a Standard Deviation value?
Outliers are scores that are significantly distant from the mean. Outliers can heavily influence the mean used to calculate standard deviation. If the standard deviation is high and outliers are present, that may mean the standard deviation does not represent the typical value.
Cronbach’s Alpha
What is Cronbach’s Alpha?
Cronbach’s Alpha is an internal consistency measurement that estimates the reliability of a quiz. Values range from 0 to 1, with higher values indicating greater reliability.
Note: Since Cronbach’s Alpha is measuring internal consistency, randomized items would distort the value, so all randomized items in a quiz are excluded.
How is it calculated?
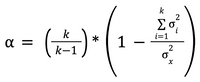 Cronbach's Alpha Formula
Cronbach's Alpha Formula
where 𝑘 is the number of questions, 𝜎ᵢ² is the variance of i-th question scores, and 𝜎ₓ² is the variance of the quiz.
How do I interpret and evaluate a Cronbach’s Alpha value?
Values range from 0 to 1, with higher values indicating greater internal consistency and reliability, meaning the items are strongly correlated and measure the same underlying construct. A value of zero indicates that there is no correlation between the items at all and that they are totally independent from each other. Knowing the answer to one item doesn’t correlate to knowledge needed to accurately answer another item in the quiz.
While there isn’t a strict threshold, a value of 0.70 or higher is considered acceptable. Lower values may be acceptable if the quiz measures a complex topic.
You can assess the corrected item-total correlation coefficient to identify items that might be less correlated to the underlying construct being measured. Removing such items could improve Cronbach’s Alpha.
Limitations
Cronbach’s Alpha assesses internal consistency, but does not guarantee validity, nor does it address quality.
Individual Item Statistics
Mean Earned Points
Displays the average point score achieved among students who were given the item.
Median Earned Points
Displays the middle value of point scores achieved among students who were given the item when all scores are arranged in ascending order. Unlike the mean score, which can be influenced by extreme values, the median is not affected by outliers.
Item Difficulty
What is Item Difficulty?
Item difficulty (also known as p-value) is the proportion of participants who answered the item correctly. Values range from 0 (nobody answered correctly) to 1 (everyone answered correctly).
Note: Calculating the item difficulty operates as a dichotomous question and ignores partial credit or points.
How is it calculated?
Item Difficulty is calculated by dividing the number of participants who answered the item correctly by the total number of participants. In the case of randomized items, the total number of participants include only the students who received the item as part of their quiz.
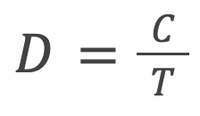 Item Difficulty Formula
Item Difficulty Formula
where 𝐶 is the number of students who answered correctly and 𝑇 is the total number of students.
How do I interpret and evaluate an Item Difficulty value?
An item difficulty value close to 1 means that most students answered the item correctly, which might indicate that the item is considered easy for students or might not effectively challenge the students. This might be the intended expectation if an item is used to test mastery. A value closer to 0 suggests that few participants answered the item correctly, which might indicate that the item is challenging for students.
While there is no strict threshold, generally items with item difficulty values below 0.30 are considered too challenging and values above 0.85 considered too easy. If the item difficulty is too high or too low, consider adjusting the item or reviewing the wording to better match the intended difficulty level.
Like any proportion or percentage, the sample size used can greatly influence the item difficulty metric. When the sample size is small, a few submissions can greatly change the value whereas when the sample size is large, it takes more submissions with the same score/value to change the overall item difficulty.
Note: To get a more cohesive picture of an item, consider assessing the discrimination index and the corrected item-total correlation coefficient.
Correlational Calculations
The following calculations help to better understand how individual items relate or correlate to the total score awarded for the quiz and to the other items in the quiz.
Corrected Item-total Correlation Coefficient
What is the Corrected Item-total Correlation Coefficient?
The corrected item-total correlation coefficient is the value of the Pearson correlation obtained when an item score is correlated with the total score of the quiz from which that item is contained. The correction to that value comes in when the item being correlated is removed from the calculated total score to remove bias; accounting for an item only once rather than twice in the metric. Modern measurement practitioners (i.e. psychometricians and assessment evaluation experts) tend to use this metric more often than the discrimination index due to the fact that it incorporates the entire score scale rather than focusing only on the highest and lowest values in the score range.
Essentially, this metric helps determine if the students who are answering the item correctly (or scoring higher on an item than other students) tend to be the individuals who score higher on the rest of the quiz. Or conversely, showing if those who perform poorly on an item tend also to not do as well on the rest of the quiz.
How is it calculated?
The corrected item-total score correlation coefficient is calculated by dividing the covariance of the item score and the test score (minus the item in question; the corrected total score) by the product of the standard deviation of the item and the standard deviation of the corrected total score:
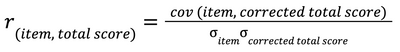 Corrected Item-total Correlation Coefficient Formula
Corrected Item-total Correlation Coefficient Formula
where cov (item, corrected total score) is the covariance of the item and the corrected total score:
cov(item, corrected total score) = 𝑛∑(item)(corrected total score - (∑ item)(∑ corrected total score)
How do I interpret and evaluate the Corrected Item-total Correlation Coefficient value?
This value, like other correlation coefficients, ranges from -1 to +1. Ideally, items should aim to obtain values greater than or equal to +.20. Values near 0 indicate little to no relationship between item performance and performance on the rest of the test. Negative values are indicative of unexpected behavior (e.g. those who do well on an item tend to score lower on the rest of the quiz and vice versa). In a sense, this metric is considered a more comprehensive and sensitive measure of discrimination.
Discrimination Index
What is Discrimination Index?
The discrimination index is focused on how well an item differentiates between the highest and lowest scoring individuals. It ranges from -1 to +1. A higher value suggests good discrimination while a lower (or negative) value indicates poor discrimination.
How Is It Calculated?
To calculate the discrimination index, the students who took the quiz rank percentile ranks based on the scores are calculated, and students are then classified into 3 groups: Students at or below the 27th percentile, students at or above the 63rd percentile, and everyone in between. Item difficulty (p value) is calculated for the upper and lower groups. The discrimination is the difference between the upper group item difficulty and the lower group difficulty.
How do I interpret and evaluate the Discrimination Index value?
Similar to the corrected item-total correlation coefficient, a high discrimination index indicates that the individuals who perform well on the test tend to perform well on the particular item. A lower discrimination index value means the item is not discriminating well. A negative number means there is a reversed/unexpected relationship. Thresholds for value ranges vary, but a general set of guidelines is:
|
Discrimination index
|
Interpretation
|
|
0.40 and above
|
Very good discrimination
|
|
0.30 - 0.39
|
Good discrimination
|
|
0.20 - 0.29
|
Fair discrimination
|
|
0.10 - 0.19
|
Not discriminating
|
|
Below 0.10
|
Poor item
|
|
Negative
|
Reversed relationship
|
CSV Files and JSON Objects
How do I interpret and evaluate the CSV File for New Quizzes Quiz and Item Analysis?
The CSV file for New Quizzes’ Quiz and Item Analysis report includes the same information as you can see in Canvas interface.
Notes:
- Unlike the Canvas interface, metrics are not rounded in the CSV file.
- If a field can’t be calculated (e.g.: Cronbach’s Alpha), a “N/A” string is added to the cell.
- If a field is not available in the report (e.g., “No answer” student count for categorization question type), a “Not supported” string is added to the cell.
The CSV file name is the quiz title and “Quiz and Item Analysis Report” string.
The first nine columns are reserved for the quiz analysis and only one row is filled.
 View CSV File Example
View CSV File Example
The column headings are as follows:
ReportGenerated: Date and time when the report was generated
QuizTitle: Title of the quiz
QuizHighScore: High score
QuizLowScore: Low score
QuizMeanScore: Mean score
QuizMedianScore: Median Score
QuizStandardDeviation: Standard Deviation
QuizCronbachsAlpha: Cronbach’s Alpha
QuizMeanElapsedTime: Mean Elapsed Time
From column ten to the end, the first row is always empty. Then each row represents one item in the quiz.
 View CSV File Items Example
View CSV File Items Example
The column headings are as follows:
ItemID: ID of the quiz item
Title: Title of the item
ItemDifficulty: Item Difficulty
PossiblePoints: Maximum Points Possible
MeanEarnedPoints: Mean Earned Points
MedianEarnedPoints: Median Earned Points
DiscriminationIndex: Discrimination Index
CorrectedItemTotalCorrelation: Corrected Item Total Correlation Coefficient
ItemType: Question Type
Correct: Number of students who answered the item correctly
Incorrect: Number of students who answered the item incorrectly
NoResponse: Number of students who didn’t answer the item
AnswerFrequencies: Representation of the Answer Frequency Summary table
How do I read and interpret the AnswerFrequencies column?
The Answer Frequency Summary table is represented in JSON (JavaScript Object Notation) objects due to the complexity of the data. Learn more about JSON.
The following JSON object is a representation of a categorization question:
{
"answers": [
{
"answer": "Sunglasses",
"categories": [
{
"category": "_distractors_",
"count": 4,
"correct": true
},
{
"category": "Essentials",
"count": 1,
"correct": false
},
{
"category": "Add-ons",
"count": 1,
"correct": false
}
]
},
{
"answer": "Light source",
"categories": [
{
"category": "_distractors_",
"count": 1,
"correct": false
},
{
"category": "Essentials",
"count": 2,
"correct": false
},
{
"category": "Add-ons",
"count": 3,
"correct": true
}
]
},
{
"answer": "Regulator",
"categories": [
{
"category": "_distractors_",
"count": 0,
"correct": false
},
{
"category": "Essentials",
"count": 5,
"correct": true
},
{
"category": "Add-ons",
"count": 1,
"correct": false
}
]
},
{
"answer": "Mask",
"categories": [
{
"category": "_distractors_",
"count": 0,
"correct": false
},
{
"category": "Essentials",
"count": 5,
"correct": true
},
{
"category": "Add-ons",
"count": 1,
"correct": false
}
]
}
]
}
The “answers” field is a list of objects.
Each answer has the same fields: the “answer” (the text of the answer) and “categories” (a list of objects).
A category object has three fields:
- the “category” field is the name of category you created
- the “count” field shows how many students added answers to this category
- the “correct” field tells if the answer is set to this category as correct
Note: You can see “category”: “_distractors_” at every answer object. This is for the Additional Distractors with a pre and postfix sign, to avoid confusion if you use the “Disctractors” name as one of your category in your question.