Community help

jared_flaherty · ‎05-24-2018

Hi-

I'm using the GET /v1/courses/{course_id}/assignments API on a course and it times out with a 504 Response Code.

I can run the same API call on many other courses without issue.

There are only 8 graded discussions in the course. No quizzes, no assignment assignments, etc.

Any ideas on what could be causing the timeout?

James · ‎05-25-2018

@jared_flaherty ,

Here's my follow-up with a recommended solution that can maintain accessibility near the end.

I took the code you supplied, cleaned up the mangling that Jive had done to it, and put it into a new course inside our beta instance so that it was the only thing there. The images came through fine. I uploaded my own file and then linked to it for the attachment at the end. I had to make it a graded discussion to get it to show up in the assignments list, but once I did that, I was ready to test.

It took 4212.37 ms (4.2 s) to download it. That is exceptionally long, even for the beta instance. By comparison fetching 91 assignments from my spring statistics course took 7503.48 seconds, but fetching just a single assignment took 972.86 ms.

What I noticed is that the content of the discussion question was included twice. It's there as the description of the assignment and there as discussion_topic.message.

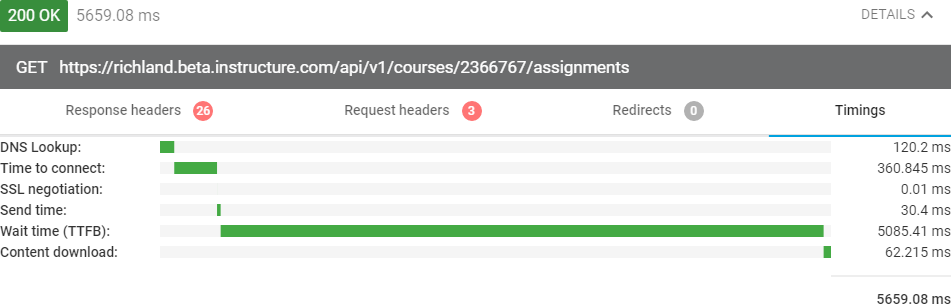
I ran it again and it took 5659.08 ms to download your discussion question. The timings screen shows that most of that time was spent waiting on Canvas.

I went in and duplicated the assignment so now I had the discussion twice. It now took 11,925.76 ms to download. 11,691.305 ms of that was spent waiting on Canvas to gather the assignment together.

You can probably see where this is going. Repeated loads dropped this down to 6139.50 ms, but still really long

Now I wanted to see if it was equation related or just size related. I generated a Lorem Ipsum file that was about the same number of bytes as your equation discussion, but contained nothing other than paragraphs.

Amazingly, when just the Lorem Ipsum discussion was loaded, the load time dropped to 776.36 ms. It does seem to have something to do with the content, not just the amount of the content.

Stripping out the list of questions from the Unit Questions section (where all of the equations are) dropped the retrieval time for the assignment to 642.81 ms.

I put all of the questions back except for 18, which I noticed had some styling with font codes and other things that the others didn't. It wasn't a standard Canvas equation object. The fetch time was 2726.72 ms, so that didn't seem to be the deciding factor.

I then took out all questions after 4. That was the first one that had any equation object in it. This dropped the fetch time to 2168.45 ms. Faster, but still longer than without any equations.

Keeping just those 4 equations, I edited each one using the equation editor and immediately saved it without changing anything. Now the download time dropped to 1283.48 ms. That's almost twice as fast.

When I got looking into what had changed, it turns out that I had inadvertently used our production instance for the equation URLs and editing them changed them to the beta instance. I'm not going to go through and redo the analysis. I did change all the production URLs to beta URLs and I was back to 8125.23 ms the first time I fetched it and 2905.53 ms the second time. That wasn't the issue and you're not getting the benefit of loading from a cache as you're only making the initial load and then it's timing out.

I'm kind of glad to see this because I'm going to recommend that you do something that I did this spring without hard justification, it just felt right. I had noticed in the past that the assignment instructions got downloaded through the API -- a lot, so I made a decision to shorten the assignment directions and put them on a separate page. The students didn't really like it and said they missed the directions because it was on a separate page. They then turned around and shot their argument in the foot by saying the instructions were too long and so they couldn't follow all of it. My point was that if they're too long, they're too long on the discussion page and they push all the other stuff off the page so they have to do lots of scrolling to find each other's responses.

What I would suggest is putting the directions for the discussion on a separate page -- perhaps in a PDF file so if you need to set the availability. Then, in the discussion itself, you let the students know that the instructions are contained in a separate document. The body of the assignment is just a couple of links to internal files and loads quickly and your discussions don't time out.

The instructions the professor gave were way too long to be on the discussion page anyway -- especially since they're something that the students need to do before they can complete the discussion.

If I were you, I would also consider filing a trouble ticket with Canvas that when equations are included in a discussion, it makes the assignment load slowly. The problem does seem to exist for any assignment that has equations in it, not just discussions. I took the HTML from the discussion and pasted it into a regular assignment and it took 1666.03 ms, about half the time it does for a discussion. That means that whatever processing they're doing that's slowing things down is repeated for the assignment.description and the discussion.message.

Again, I did all of my testing in the beta instance and it might have something different than the production instance. It's certainly normally slower, but it shouldn't be that much slower (relatively speaking).

View solution in original post

stuart_ryan · ‎05-24-2018

Hi @jared_flaherty ,

That is a conundrum. May I ask, does it timeout 100% of the time or only on occasion?

If it is something that works on all other courses, and fails 100% of the time, then I would suggest this is something that Canvas Support would need to investigate for you.

I am wondering if you have had a chance to go through any of the troubleshooting steps on https://community.canvaslms.com/docs/DOC-14390-canvas-apis-getting-started-the-practical-ins-and-out...

Specifically, I would be curious if you get the same error in the Canvas Live API (it never hurts to check). There is also some good guidance on things you can collect to give Canvas Support the info they need to troubleshoot the issue further.

From what you have told me, it feels like there might be a bug at play, but never hurts to be thorough and check these few things first to understand the symptoms more.

Hope that helps and look forward to hearing from you.

Stuart

jared_flaherty · ‎05-24-2018

Thanks, Stuart-

I actually am using the LIVE API on this. So, more details have arisen today since my post. The instructor of this course reported having issues with Pearson MyLabs not syncing back into Canvas. I spent some time troubleshooting some things and couldn't get it working. I decided to remove the discussion assignments from the course, as they were causing issue with the API already. When I removed the discussions the grade sync from MML worked perfectly. I put the discussions back in the course and the grade sync wouldn't work. So, there is something in these discussions that is causing issues with APIs. The discussions have a bunch of images of math equations in them... the user that placed the images in the discussion descriptions used this method:

" />] has a solution amounts to asking whether <img class="equation_image" title="b" src="https://canvas.park.edu/equation_images/b" alt="LaTeX: b" data-equation-content="b" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">

I don't know much of anything about the equation images. Any advice is appreciated.

stuart_ryan · ‎05-24-2018

Hi @jared_flaherty ,

No worries at all, always happy to throw around ideas.

That is extremely unusual, I will admit I have had zero experience with the equation images myself, though it is entirely possible there could be an issue with them.

If I go with the 'steps I would normally try when tinkering with something I have no experience with' I would suggest manually recreating the discussion posts in a new course shell, and see if the problem persists. If you do it one by one, you can narrow down to if there is a problem with a single one of them, or if it affects all five equally.

If there is a bug, this can help ascertain the extent. Also, it may shed light on the process more where you can see if there are any unusual characters etc.

Depending on the content (and sensitivity etc), I would be curious to get an export of a course shell with the five discussions (after you have isolated them in a new course and confirmed they are the cause). I can then have a quick eyeball if you would like and see if anything springs to mind. (Happy for you to private message this to me also if you would prefer).

Look forward to hearing from you.

Stuart

jared_flaherty · ‎05-25-2018

I believe I know the issue. The math equation images are not actually in the Canvas course but rather out somewhere else on an AWS server somehow.

This HTML calls for an math equation image

https://canvas.park.edu/equation_images/%255Cfrac%257B1%257D%257B2%257Dv_1

Which actually directs to here

https://njadnrfof9.execute-api.us-east-1.amazonaws.com/prod/svg?tex=%5Cfrac%7B1%7D%7B2%7Dv_1

Takes too long to load all of this and it times out.

Thanks for the help!

Jared

James · ‎05-25-2018

I hope that's the solution, but it doesn't sound right.

The content associated with the math equations is delivered through the API, meaning all of the MathML and extra stuff that Canvas loads to make the equations work. That might be providing more information to download than a plain text. In fact, I put my long assignments instructions into a separate document than the assignment itself this spring to help reduce the amount of information that was transferred every time the assignment information was fetched (students complained about not having the information on the same page as the discussion and other students complained about having too many instructions that they couldn't possibly absorb all of it).

However, the external site that renders and/or delivers the equations isn't invoked with the GET from the API. It is up to your user agent (normally a browser) to download and display those images and that's when the external site is referenced. What is delivered from the API is just the information necessary so it can do that.

Having a lot of equations will make the text of the assignment description longer, but it doesn't sound right that the equations being stored on an external server is the culprit.

Even though it doesn't sound right, you may be onto something. It may be that the live API is somehow trying to download those files because it's ran within a browser while a normal fetch using the API is made somewhere else. I found the live API so terribly slow and basically killed the browser so that I had to stop using it; things may be better now.

Have you tried making the API call from a REST client or program rather than through the live API? Another way to check, since this is a simple GET request, is to go to your browser and enter the API's URL in the location bar. After the canvas.park.edu, add /api/v1/courses/123/assignments and hit enter (of course, change the 123 to the actual course number).

jared_flaherty · ‎05-25-2018

Thanks, James-

We were actually alerted to the issue by Kim Munzo at ASPIREedu when the Assignment pull for Dropout Detective timed out on this course. I then used both the Live API and using by entering the APIs URL in a web browser. All with the same results.

We were then contacted by the instructor of the course with regard to the MyMathLab not being able to sync to this Canvas course. I was able to determine that the MyMathLab indeed wouldn't sync up with the Canvas course on my end (timing out) and I decided to remove the Canvas Discussion boards and voila, the sync between MyMathLab and the Canvas course worked perfectly. I put the Canvas Discussion boards back in and the MyMathLab sync failed again due to timing out. So, I removed all of the HTML that had the math equations and tested again and the MyMathLab sync worked great again.

What you say about the API calls not invoking the call for the equations makes sense and I had already been thinking that was the case.

What I do know is something in those math equations is causing the GET Assignments API to fail in the REST and LIVE APIs and they are also causing the MyMathLab sync to fail, which I'm sure uses the REST API as well.

I advised the Instructional Design team to create images of the math equations and place them in the FILES section of the Canvas course and link to them from the Discussion Descriptions. That should fix it.

I'd still like to know what is causing the issue... here is the HTML from one of the problem child discussion descriptions:

Any help is greatly appreciated!!!!

<h2>Introduction</h2>
Each unit, you will respond to one of the questions listed in the "This Unit's Questions" section below the Directions.
All respectful responses are welcome to the Discussion thread, but in order to earn the response posting points you must respond to one of your classmate's answers with a thoughtful, math concept focused posting meeting the criteria described below.
Notes:
<ol>
<li>You will not earn points for postings that contain quotes without proper punctuation and source citing. Repeated plagiarism will result in course failure, and a plagiarism incident report on your academic record. Remember this is a serious offense with possible administrative expulsion as the ultimate consequence. If you are in doubt, ask for assistance.</li>
<li>Only one response posting is eligible for earning points per unit, but you may respond to as many postings as you like.</li>
<li>Remember all thread postings should be proofread and the spellchecker tool used before posting. All college level writing, even thread postings, should be grammatically correct.</li>
</ol>
<h2>Directions</h2>
<ol>
<li>Initial Posts - Respond to one question below by 11:59 p.m. Saturday (CT).
<ol>
<li>Read through the answer postings and responses already posted by classmates.</li>
<li>Choose a discussion prompt not previously answered.
<ol>
<li>Once a discussion prompt has been addressed it is no longer eligible for you to answer, and will not earn you any points should you post an answer to it.</li>
<li>Answer it at that time. Discussion prompts cannot be reserved for answering at a later time. Should two students work simultaneously on the same discussion prompt, and post answers within minutes of each other, the second answer posted can be considered as that student's response posting. Another discussion prompt will need to be chosen and answered by that student in order to earn answer points.</li>
</ol>
</li>
<li>Include the discussion prompt question number at the very beginning of the FIRST LINE of your answer post. Type (or copy and paste) the discussion prompt as the first line(s) of your answer post. Begin typing your answer after the discussion prompt.
Use the "Insert Math Equation" tool in the Canvas thread toolbar to make adjustments for any symbols. 
Example: 1. What is the name of this course? (Not a real discussion prompt...just an example!) The name of this course is Intermediate Algebra.
</li>
</ol>
</li>
<li>Response Posts - Respond to one initial post with least two complete concept focused sentences by 11:59 p.m. Sunday (CT).
<ol>
<li>Show that you understand the concept by expanding the thoughts given in the answer posting by adding more information.</li>
<li>Rewording the thoughts given, or give an example are also ways to show your understanding or enhance the discussion of the concept. If you do not understand the concept, ask discussion prompts specifically about the concept discussed in the discussion prompt and answer.</li>
<li>Make sure your discussion prompts are related only to the discussion prompt and answer you are responding to.</li>
<li>
Please respond to incorrect or incomplete answers as well as the correct ones, tactfully completing the answer or presenting what you believe to be the correct answer.
Before you praise and agree with another's answer, you need to verify that it is correct. If the answer is incorrect and you are agreeing, your points will decrease. "I agree" or "Good answer" type sentences are not included as part of the two sentence requirement. Discussing your personal understanding of the concept is not part of the sentence count either. Also not included are sentences of appreciation for a page or website quoted in the answer. You may state that you agree or disagree, but you must go on to state why. If you merely write that the answer is good because it is correct, or because it helped you to understand the concept, it will not be considered for earning points.
</li>
</ol>
</li>
</ol>
<h2>Unit Questions</h2>
Choose one of the following questions to answer.
In Questions 1 through 18, key statements from this section are either quoted directly, restated slightly (but still true), or altered in some way that makes them false in some cases. If you choose one of these, mark it True or False, and justify your answer. If true, give the approximate location where a similar statement appears in the text or slides, or refer to the correct definition or theorem. If false, give the location of a statement that has been quoted or used incorrectly, or cite an example that shows the statement is not true in all cases.
If you choose one of the remaining questions (Questions 19 through 32) answer the question and justify your answer by citing appropriate definitions, theorems or other statements from the text or slides.
<ol>
<li>Every elementary row operation reversible.</li>
<li>A 5 × 6 matrix has six rows.</li>
<li>The solution set of a linear system involving variables <img class="equation_image" title="x_1,...,x_n" src="https://canvas.park.edu/equation_images/x_1%252C...%252Cx_n" alt="LaTeX: x_1,...,x_n" data-equation-content="x_1,...,x_n" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>x</mi>
<mn>1</mn>
</msub>
<mo>,</mo>
<mo>.</mo>
<mo>.</mo>
<mo>.</mo>
<mo>,</mo>
<msub>
<mi>x</mi>
<mi>n</mi>
</msub>
</math>" /> is a list of numbers (<img class="equation_image" title="s_1,...,s_n" src="https://canvas.park.edu/equation_images/s_1%252C...%252Cs_n" alt="LaTeX: s_1,...,s_n" data-equation-content="s_1,...,s_n" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>s</mi>
<mn>1</mn>
</msub>
<mo>,</mo>
<mo>.</mo>
<mo>.</mo>
<mo>.</mo>
<mo>,</mo>
<msub>
<mi>s</mi>
<mi>n</mi>
</msub>
</math>" />) that makes each equation in the system a true statement when the values are substituted for <img class="equation_image" title="s_1,...,s_n" src="https://canvas.park.edu/equation_images/s_1%252C...%252Cs_n" alt="LaTeX: s_1,...,s_n" data-equation-content="s_1,...,s_n" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>s</mi>
<mn>1</mn>
</msub>
<mo>,</mo>
<mo>.</mo>
<mo>.</mo>
<mo>.</mo>
<mo>,</mo>
<msub>
<mi>s</mi>
<mi>n</mi>
</msub>
</math>" /> are substituted for <img class="equation_image" title="x_1,...,x_n" src="https://canvas.park.edu/equation_images/x_1%252C...%252Cx_n" alt="LaTeX: x_1,...,x_n" data-equation-content="x_1,...,x_n" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>x</mi>
<mn>1</mn>
</msub>
<mo>,</mo>
<mo>.</mo>
<mo>.</mo>
<mo>.</mo>
<mo>,</mo>
<msub>
<mi>x</mi>
<mi>n</mi>
</msub>
</math>" /> respectively.</li>
<li>Two matrices are row equivalent if they have the same number of rows.</li>
<li>Elementary row operations on an augmented matrix never change the solution set of the associated linear system.</li>
<li>In some cases, a matrix may be row reduced to more than one matrix in reduced echelon form, using different sequences of row operations.</li>
<li>The row reduction algorithm applies only to augmented matrices for a linear system.</li>
<li>A basic variable in a linear system is a variable that corresponds to a pivot column in the coefficient matrix.</li>
<li>If every column of an augmented matrix contains a pivot, then the corresponding system is consistent.</li>
<li>The pivot positions in a matrix depend on whether row interchanges are used in the row reduction process.</li>
<li>A general solution of a system is an explicit description of all solutions of the system.</li>
<li>Whenever a system has free variables, the solution set contains many solutions.</li>
<li>An example of a linear combination of vectors <img class="equation_image" title="v_1" src="https://canvas.park.edu/equation_images/v_1" alt="LaTeX: v_1" data-equation-content="v_1" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>v</mi>
<mn>1</mn>
</msub>
</math>" /> and <img class="equation_image" title="v_2" src="https://canvas.park.edu/equation_images/v_2" alt="LaTeX: v_2" data-equation-content="v_2" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>v</mi>
<mn>2</mn>
</msub>
</math>" /> is the vector <img class="equation_image" title="\frac{1}{2}v_1" src="https://canvas.park.edu/equation_images/%255Cfrac%257B1%257D%257B2%257Dv_1" alt="LaTeX: \frac{1}{2}v_1" data-equation-content="\frac{1}{2}v_1" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mfrac>
<mn>1</mn>
<mn>2</mn>
</mfrac>
<msub>
<mi>v</mi>
<mn>1</mn>
</msub>
</math>" />.</li>
<li>The solution set of the linear system whose augmented matrix is [<img class="equation_image" title="a_1\:a_2\:a_3\:b" src="https://canvas.park.edu/equation_images/a_1%255C%253Aa_2%255C%253Aa_3%255C%253Ab" alt="LaTeX: a_1\:a_2\:a_3\:b" data-equation-content="a_1\:a_2\:a_3\:b" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mn>1</mn>
</msub>
<mspace width="mediummathspace" />
<msub>
<mi>a</mi>
<mn>2</mn>
</msub>
<mspace width="mediummathspace" />
<msub>
<mi>a</mi>
<mn>3</mn>
</msub>
<mspace width="mediummathspace" />
<mi>b</mi>
</math>" />] is the same a the solution set of the equation <img class="equation_image" title="x_1a_1+\:x_2a_2\:+\:x_3a_3\:=b" src="https://canvas.park.edu/equation_images/x_1a_1%252B%255C%253Ax_2a_2%255C%253A%252B%255C%253Ax_3a_3%2..." alt="LaTeX: x_1a_1+\:x_2a_2\:+\:x_3a_3\:=b" data-equation-content="x_1a_1+\:x_2a_2\:+\:x_3a_3\:=b" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>x</mi>
<mn>1</mn>
</msub>
<msub>
<mi>a</mi>
<mn>1</mn>
</msub>
<mo>+</mo>
<mspace width="mediummathspace" />
<msub>
<mi>x</mi>
<mn>2</mn>
</msub>
<msub>
<mi>a</mi>
<mn>2</mn>
</msub>
<mspace width="mediummathspace" />
<mo>+</mo>
<mspace width="mediummathspace" />
<msub>
<mi>x</mi>
<mn>3</mn>
</msub>
<msub>
<mi>a</mi>
<mn>3</mn>
</msub>
<mspace width="mediummathspace" />
<mo>=</mo>
<mi>b</mi>
</math>" /></li>
<li>When <img class="equation_image" title="u" src="https://canvas.park.edu/equation_images/u" alt="LaTeX: u" data-equation-content="u" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>u</mi>
</math>" /> and <img class="equation_image" title="v" src="https://canvas.park.edu/equation_images/v" alt="LaTeX: v" data-equation-content="v" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>v</mi>
</math>" /> are nonzero vectors. The set Span<img class="equation_image" title="\lbrace u,v\rbrace" src="https://canvas.park.edu/equation_images/%255Clbrace%2520u%252Cv%255Crbrace" alt="LaTeX: \lbrace u,v\rbrace" data-equation-content="\lbrace u,v\rbrace" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mo fence="false" stretchy="false">{</mo>
<mi>u</mi>
<mo>,</mo>
<mi>v</mi>
<mo fence="false" stretchy="false">}</mo>
</math>" /> is always visualized as a plane through the origin.</li>
<li>When <img class="equation_image" title="u" src="https://canvas.park.edu/equation_images/u" alt="LaTeX: u" data-equation-content="u" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>u</mi>
</math>" /> and <img class="equation_image" title="v" src="https://canvas.park.edu/equation_images/v" alt="LaTeX: v" data-equation-content="v" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>v</mi>
</math>" /> are nonzero vectors. The set Span<img class="equation_image" title="\lbrace u,v\rbrace" src="https://canvas.park.edu/equation_images/%255Clbrace%2520u%252Cv%255Crbrace" alt="LaTeX: \lbrace u,v\rbrace" data-equation-content="\lbrace u,v\rbrace" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mo fence="false" stretchy="false">{</mo>
<mi>u</mi>
<mo>,</mo>
<mi>v</mi>
<mo fence="false" stretchy="false">}</mo>
</math>" /> contains only the line through <img class="equation_image" title="u" src="https://canvas.park.edu/equation_images/u" alt="LaTeX: u" data-equation-content="u" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>u</mi>
</math>" /> and the origin, and the line through <img class="equation_image" title="v" src="https://canvas.park.edu/equation_images/v" alt="LaTeX: v" data-equation-content="v" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>v</mi>
</math>" /> and the origin.</li>
<li>Asking whether the linear system corresponding to an augmented matrix [<img class="equation_image" title="a_1\:a_2\:a_3\:b" src="https://canvas.park.edu/equation_images/a_1%255C%253Aa_2%255C%253Aa_3%255C%253Ab" alt="LaTeX: a_1\:a_2\:a_3\:b" data-equation-content="a_1\:a_2\:a_3\:b" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mn>1</mn>
</msub>
<mspace width="mediummathspace" />
<msub>
<mi>a</mi>
<mn>2</mn>
</msub>
<mspace width="mediummathspace" />
<msub>
<mi>a</mi>
<mn>3</mn>
</msub>
<mspace width="mediummathspace" />
<mi>b</mi>
</math>" />] has a solution amounts to asking whether <img class="equation_image" title="b" src="https://canvas.park.edu/equation_images/b" alt="LaTeX: b" data-equation-content="b" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>b</mi>
</math>" /> is in Span<img class="equation_image" title="\lbrace a_1,\:a_2,\:a_3\rbrace" src="https://canvas.park.edu/equation_images/%255Clbrace%2520a_1%252C%255C%253Aa_2%252C%255C%253Aa_3%255C..." alt="LaTeX: \lbrace a_1,\:a_2,\:a_3\rbrace" data-equation-content="\lbrace a_1,\:a_2,\:a_3\rbrace" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mo fence="false" stretchy="false">{</mo>
<msub>
<mi>a</mi>
<mn>1</mn>
</msub>
<mo>,</mo>
<mspace width="mediummathspace" />
<msub>
<mi>a</mi>
<mn>2</mn>
</msub>
<mo>,</mo>
<mspace width="mediummathspace" />
<msub>
<mi>a</mi>
<mn>3</mn>
</msub>
<mo fence="false" stretchy="false">}</mo>
</math>" />.</li>
<li>The vector <img class="equation_image" style="max-width: 100%; height: auto; vertical-align: middle; border: 0px; color: #2d3b45; font-family: LatoWeb, 'Helvetica Neue', Helvetica, Arial, sans-serif; font-size: 16px; font-style: normal; font-weight: 400; text-align: left; text-indent: 0px; white-space: normal; background-color: #ffffff;" title="v" src="https://canvas.park.edu/equation_images/v" alt="LaTeX: v" data-equation-content="v" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>v</mi>
</math>" /> results when a vector <img class="equation_image" title="u-v" src="https://canvas.park.edu/equation_images/u-v" alt="LaTeX: u-v" data-equation-content="u-v" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>u</mi>
<mo>&#x2212;</mo>
<mi>v</mi>
</math>" /> is added to the vector <img class="equation_image" title="v" src="https://canvas.park.edu/equation_images/v" alt="LaTeX: v" data-equation-content="v" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>v</mi>
</math>" />.</li>
<li>What are the two fundamental questions about a linear system?</li>
<li>Why are equivalent linear systems useful or important?</li>
<li>What is the difference between consistent and inconsistent linear systems?</li>
<li>What is a parametric description of the solution set of a linear system and why do we call it a parametric description?</li>
<li>What does it mean if one row in an echelon form of an augmented matrix is [0 0 0 5 0] and why?</li>
<li>Suppose the coefficient matrix of a linear system of four equations in four variables has a pivot in each column. Explain why the system has a unique solution.</li>
<li>Suppose a system of linear equations has a 3 × 5 augmented matrix whose fifth column is not a pivot column. Is the system consistent? Why or why not?</li>
<li>Suppose the coefficient matrix of a system of linear equations has a pivot position in every row. Explain why the system is consistent.</li>
<li>Suppose a system of linear equations has a 3 × 5 coefficient matrix whose fifth column is not a pivot column. Is the system consistent? Why or why not?</li>
<li>Restate the last sentence in Theorem 2 using the concept of pivot columns: “If a linear system is consistent, then the solution is unique exactly when _______________”</li>
<li>What would you have to know about the pivot columns in an augmented matrix in order to know that the linear system is consistent and has a unique solution?</li>
<li>A system of linear equations with fewer equations than unknowns is sometimes called an underdetermined system. Can such a system have a unique solution? Explain.</li>
<li>Give an example of an inconsistent system of two equations in three unknowns.</li>
<li>A system of linear equations with more equations than unknowns is sometimes called an overdetermined system. Can such a system be consistent? Illustrate your answer with a specific system of three equations in two unknowns.</li>
</ol>
Review: <a id="" class=" instructure_scribd_file instructure_file_link" title="Week 1 Discussion Questions.docx" href="https://canvas.park.edu/courses/5933/files/94280/download?wrap=1" data-api-endpoint="https://canvas.park.edu/api/v1/courses/5933/files/94280" data-api-returntype="File">Unit 1 Discussion Questions.docx</a>

James · ‎05-25-2018

@jared_flaherty ,

That's a lot of MathML.

I advised the Instructional Design team to create images of the math equations and place them in the FILES section of the Canvas course and link to them from the Discussion Descriptions. That should fix it.

This will probably result in reduced accessibility since it won't have the MathML included.

Let's hope we can figure something else out so we can have the best of both worlds (API working and accessibility).

I'll see if I can replicate the problem on my end. I hope that the Jive software used in the Community hasn't mangled it too much.

In the meantime, have you tried fetching a specific assignment, rather than all of them, to see if that works? Maybe it was just one assignment that was causing the problem.

James · ‎05-25-2018