In that case, wouldn't -.637 then "round up" to -.63 and -.632 "round down" to -.64? That doesn't seem to make any sense to me.
I was talking only about the values that are equidistant -- where the next digit is a 5. -0.637 is closer to -0.64. -0.632 is closer to -0.63. There is no ambiguity there with rounding.
If you want to force a directional round, use the floor() or ceil() functions.
It also makes the most sense to have it cut down the middle: half of the digits round one way and the other half round the other, but according to Canvas/JavaScript, 6 of the digits round down in absolute value and 4 round up.
This is incorrect. If you are rounding to 2 decimals and looking at the 3rd decimal to decide where to round, then 0, 1, 2, 3, 4 (5 digits) will round down and 5, 6, 7, 8, 9 (5 digits) will round up.
I guess I just don't understand WHY JavaScript would define rounding the .5 in the direction of positive infinity.
They didn't ask me when they developed it, but I'm sure some people a lot smarter than me chimed in. Or it might have just been that the they did what they were familiar with.
From a numerical perspective, it makes for consistency,
[-2.5, -1.5) => -2
[-1.5, -0.5) => -1
[-0.5, 0.5) => 0
[0.5, 1.5) => 1
[1.5, 2.5) => 2
Rounding away from 0 makes it
(-2.5, -1.5] => -2
(-1.5, -0.5] => -1
(-0.5, 0.5) => 0
[0.5, 1.5) => 1
[1.5, 2.5) => 2
Back in the old days -- for languages that didn't support a round() function, we used int(x+0.5), which rounds up if the next digit is 5 or greater.
Some people like the round away from 0 because it is "easier" (their word) for people to understand. When following the JavaScript rule, -0.5xxxxx (where x is not all 0) rounds to -1, but -0.5 rounds to 0.
Personally, I think much of the confusion is because of well-meaning rules designed for youngsters but people took them as gospel later on. For example, when you tell people to "go to the nearest integer unless the next digit is a 5 and then round up" they probably didn't have any negative numbers. So saying "round away from 0 when the next digit is a 5" is complicated when you only have positive numbers.
Later in life, we find out that many of those rules they gave us early on aren't really true in all cases. You cannot take the square root of a negative (until you find out about complex numbers), you cannot leave a square root in the denominator (really? it makes calculus a lot easier), and my personal favorite that happened when someone was teaching variation problems "is means equals" (in statistics, "is" is a verb and it really matters what else is in the sentence, like "is more than" or "is not").
For what it's worth, Excel does round away from 0.
Does anyone know of a way I can get around this, or will I just be forced to manually check every time a student has a negative number rounded the other way?
Sure.
I sometimes ignore the sign and work on the absolute value of the number in some of the stuff I do. For example, when pretty-printing an expression with multiple terms, I decide whether to use a + or - based on the sign and then format the absolute value of the number.
That is exactly a trick that will work to round away from 0 when the number is exactly in the middle.
If [x] is your variable and you want to round to 2 decimal places and you want to round away from 0, then use this formula. Set the number of decimal places to 2.
if(x,x/abs(x)*round(100*abs(x))/100,0)
Here's the explanation.
- The if() function is really an if(boolean expression,true,false). JavaScript considers any number other than 0 to be true. It will be true and execute the first part when x is anything other than 0 and false and execute the second part when x is 0.
- x/abs(x) is a poor man's signum function. Canvas doesn't have one, but x/|x| is -1 when x < 0 and it is +1 when x > 0. It is undefined when x = 0, but this will never happen because the conditional is false when x = 0.2
- round(100*abs(x))/100 multiplies the number by 100 because round() only rounds to an integer, rounds it, and then divides it by 100. If you want 2 decimal places, multiply by 100, round, and then divide by 100. If you want 3 decimal places, then use 1000.
- 0 as the last part is because 0 rounds to 0.
Now, try x = -0.635.
- if(-0.645, ..., ...) is not 0, so it evaluates as true.
- -0.635/abs(-0.635) = -1
- round(100*abs(-0.635))/100 = round(63.5)/100 = 64/100 = 0.64
- then multiply the -1 by 0.64 to get -0.64.
Here is is in action.
x = -0.635 => -0.64
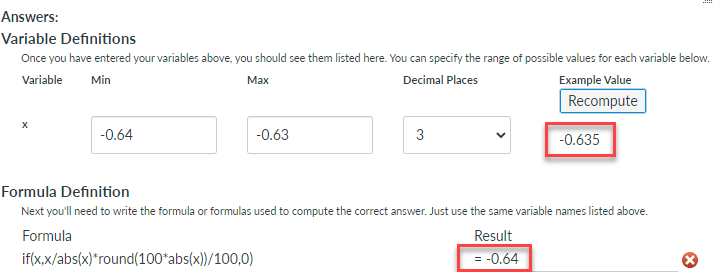
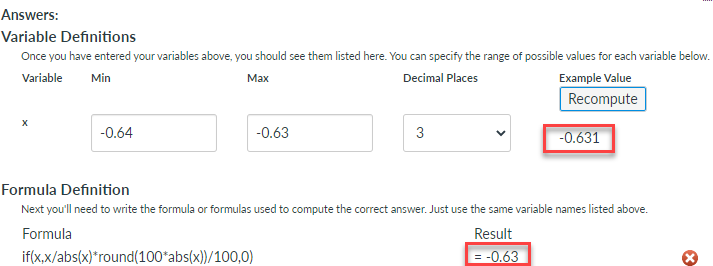
x = -0.631 => -0.63
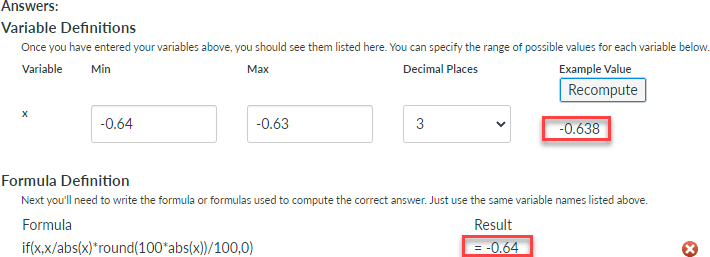
x = -0.638 => -0.64
Whatever you do, make sure the students are on the same page as you. My students who understood thing the rule they have been given would round -0.635 to -0.63. Those who round to -0.64 would do so because they think -0.64 is bigger than -0.63 and they are actually rounding up by picking it. So they would be getting it right for the wrong reason.




This discussion post is outdated and has been archived. Please use the Community question forums and official documentation for the most current and accurate information.