Why does Canvas not round negative numbers ending in 5 correctly in formula questions?

[dsmith19]

Why does Canvas not round negative numbers ending in 5 correctly in formula questions? It will round -.5 to 0, or -.635 to -.63, it's very frustrating to have Canvas mark the answers as wrong because the student rounded correctly and Canvas did not. This is the only instance that I've seen Canvas round incorrectly.

[James · Accepted solution]

 @dsmith19  

What rounding rules are you using? There are many of them to choose from.

The one I hear most often, and that we teach our students in school around here (Central Illinois), is to look at the next digit and if it is a 4 or less, round down; if it is a 5 or higher, round up.

Following that rule, if I wanted to round -0.635 to 2 decimal places, then I would look at the 5 in the thousandths place and say I should round up. When I round up -0.635, I get -0.63. To get -0.64 would be rounding down.

The same thing with -0.5. 0 is bigger than -0.5 (round up), while -1 is less than -0.5 (round down).

The IEEE 754 standard for floating-point arithmetic defines five types of rounding. It was designed to address many differences between languages in rounding. They support ties going towards the even number (-0.5 goes to 0 but -0.635 goes to -0.64), rounding ties away from zero (negative numbers round down while positive numbers round up), and three types of directed roundings (truncation, ceiling, and floor). Strangely, it doesn't mention what we teach in our schools.

Some computer languages support rounding away from 0, which is what it seems you want. JavaScript, which is the language used in the browser which is where the formula questions are generated, uses the rule I am most familiar with.

Math.round() - JavaScript | MDN 

If the fractional portion of the argument is greater than 0.5, the argument is rounded to the integer with the next higher absolute value. If it is less than 0.5, the argument is rounded to the integer with the lower absolute value. If the fractional portion is exactly 0.5, the argument is rounded to the next integer in the direction of +∞. Note that this differs from many languages' round() functions, which often round this case to the next integer away from zero, instead giving a different result in the case of negative numbers with a fractional part of exactly 0.5.

What I do with formula questions is never round and then specify a tolerance. If I have an exact answer of -0.635 and allow a tolerance of 0.005, then both -0.63 and -0.64 would be considered correct.

Another possibility with -0.635 is the inability to exactly represent a decimal number in binary. It may be -0.63500000001 or -0.63499999999 instead of -0.635. If it was -0.63499999999, then it would round to be -0.63. That doesn't explain the -0.5, which can be represented exactly. However, the JavaScript rules for rounding do explain the behavior.

[dsmith19]

You wrote:

"The one I hear most often, and that we teach our students in school around here (Central Illinois), is to look at the next digit and if it is a 4 or less, round down; if it is a 5 or higher, round up.

Following that rule, if I wanted to round -0.635 to 2 decimal places, then I would look at the 5 in the thousandths place and say I should round up. When I round up -0.635, I get -0.63. To get -0.64 would be rounding down."

In that case, wouldn't -.637 then "round up" to -.63 and -.632 "round down" to -.64? That doesn't seem to make any sense to me.

I've only ever thought of it in terms of absolute value.

It also makes the most sense to have it cut down the middle: half of the digits round one way and the other half round the other, but according to Canvas/JavaScript, 6 of the digits round down in absolute value and 4 round up.

Thank you for explaining that it is using the JavaScript definition. Now I have my answer.

I guess I just don't understand WHY JavaScript would define rounding the .5 in the direction of positive infinity.

I don't usually like including a tolerance, because I want to make sure my students are rounding things correctly, they seem to have a big problem with knowing the difference between rounding and truncating.

Does anyone know of a way I can get around this, or will I just be forced to manually check every time a student has a negative number rounded the other way?

[James]

In that case, wouldn't -.637 then "round up" to -.63 and -.632 "round down" to -.64? That doesn't seem to make any sense to me.

I was talking only about the values that are equidistant -- where the next digit is a 5. -0.637 is closer to -0.64. -0.632 is closer to -0.63. There is no ambiguity there with rounding.

If you want to force a directional round, use the floor() or ceil() functions.

It also makes the most sense to have it cut down the middle: half of the digits round one way and the other half round the other, but according to Canvas/JavaScript, 6 of the digits round down in absolute value and 4 round up.

This is incorrect. If you are rounding to 2 decimals and looking at the 3rd decimal to decide where to round, then 0, 1, 2, 3, 4 (5 digits) will round down and 5, 6, 7, 8, 9 (5 digits) will round up.

I guess I just don't understand WHY JavaScript would define rounding the .5 in the direction of positive infinity.

They didn't ask me when they developed it, but I'm sure some people a lot smarter than me chimed in. Or it might have just been that the they did what they were familiar with.

From a numerical perspective, it makes for consistency,

[-2.5, -1.5) => -2

[-1.5, -0.5) => -1

[-0.5, 0.5) => 0

[0.5, 1.5) => 1

[1.5, 2.5) => 2

Rounding away from 0 makes it

(-2.5, -1.5] => -2

(-1.5, -0.5] => -1

(-0.5, 0.5) => 0

[0.5, 1.5) => 1

[1.5, 2.5) => 2

Back in the old days -- for languages that didn't support a round() function, we used int(x+0.5), which rounds up if the next digit is 5 or greater.

Some people like the round away from 0 because it is "easier" (their word) for people to understand. When following the JavaScript rule, -0.5xxxxx (where x is not all 0) rounds to -1, but -0.5 rounds to 0.

Personally, I think much of the confusion is because of well-meaning rules designed for youngsters but people took them as gospel later on. For example, when you tell people to "go to the nearest integer unless the next digit is a 5 and then round up" they probably didn't have any negative numbers. So saying "round away from 0 when the next digit is a 5" is complicated when you only have positive numbers.

Later in life, we find out that many of those rules they gave us early on aren't really true in all cases. You cannot take the square root of a negative (until you find out about complex numbers), you cannot leave a square root in the denominator (really? it makes calculus a lot easier), and my personal favorite that happened when someone was teaching variation problems "is means equals" (in statistics, "is" is a verb and it really matters what else is in the sentence, like "is more than" or "is not").

For what it's worth, Excel does round away from 0.

Does anyone know of a way I can get around this, or will I just be forced to manually check every time a student has a negative number rounded the other way?

Sure.

I sometimes ignore the sign and work on the absolute value of the number in some of the stuff I do. For example, when pretty-printing an expression with multiple terms, I decide whether to use a + or - based on the sign and then format the absolute value of the number.

That is exactly a trick that will work to round away from 0 when the number is exactly in the middle.

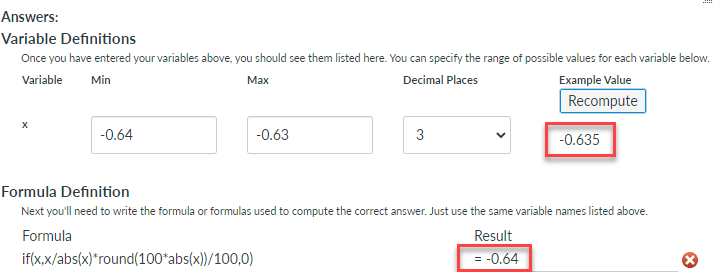
If [x] is your variable and you want to round to 2 decimal places and you want to round away from 0, then use this formula. Set the number of decimal places to 2.

if(x,x/abs(x)*round(100*abs(x))/100,0)

Here's the explanation.

• The if() function is really an if(boolean expression,true,false). JavaScript considers any number other than 0 to be true. It will be true and execute the first part when x is anything other than 0 and false and execute the second part when x is 0.
• x/abs(x) is a poor man's signum function. Canvas doesn't have one, but x/|x| is -1 when x < 0 and it is +1 when x > 0. It is undefined when x = 0, but this will never happen because the conditional is false when x = 0.2
• round(100*abs(x))/100 multiplies the number by 100 because round() only rounds to an integer, rounds it, and then divides it by 100. If you want 2 decimal places, multiply by 100, round, and then divide by 100. If you want 3 decimal places, then use 1000.
• 0 as the last part is because 0 rounds to 0.

Now, try x = -0.635.

• if(-0.645, ..., ...) is not 0, so it evaluates as true.
• -0.635/abs(-0.635) = -1
• round(100*abs(-0.635))/100 = round(63.5)/100 = 64/100 = 0.64
• then multiply the -1 by 0.64 to get -0.64.

Here is is in action.

x = -0.635 => -0.64

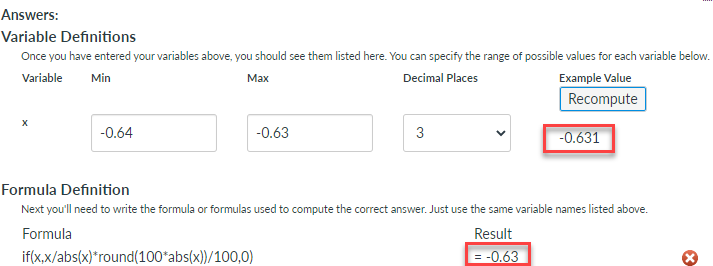
x = -0.631 => -0.63

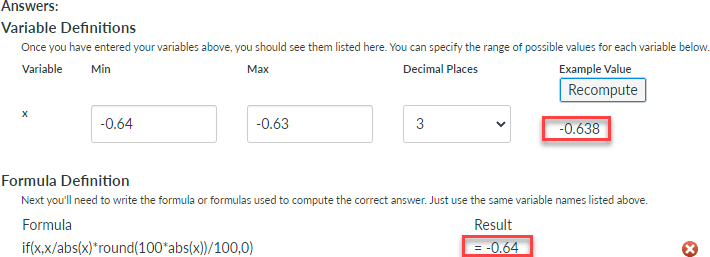
x = -0.638 => -0.64

Whatever you do, make sure the students are on the same page as you. My students who understood thing the rule they have been given would round -0.635 to -0.63. Those who round to -0.64 would do so because they think -0.64 is bigger than -0.63 and they are actually rounding up by picking it. So they would be getting it right for the wrong reason.