@Ron_Bowman wrote:
@arencambre -
That is interesting. One thing I noticed is that the format you see for the statistical information is different from mine - maybe window size as I am on a computer and you may be on a tablet (that is beside the point at hand).
I decided to look up the difference between mean and average and found the following: "Average, also called the arithmetic mean, is the sum of all the values divided by the number of values. Whereas, mean is the average in the given data. In statistics, the mean is equal to the total number of observations divided by the number of observations"
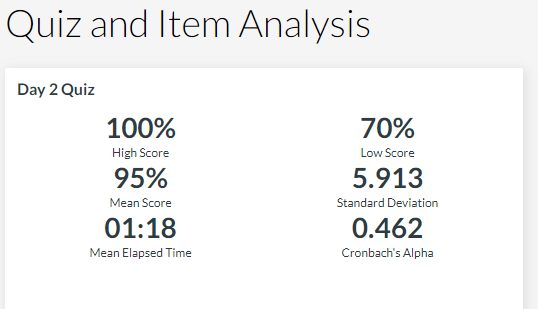
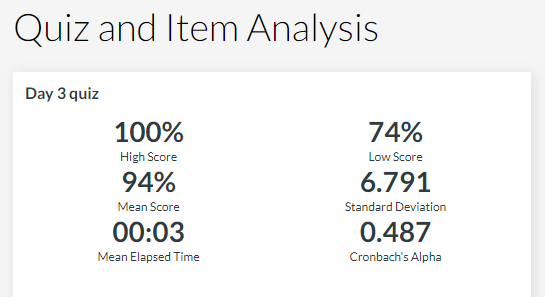
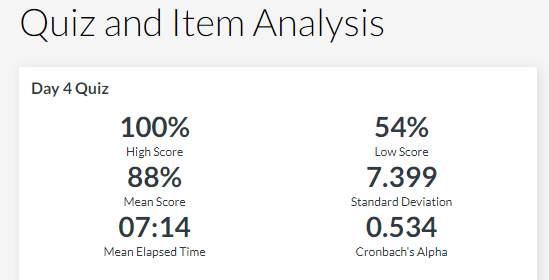
That has slightly different meanings. Just out of curiosity, how many students took the quiz for each quiz for the results shown and how many were in the class? I am wondering if there were (hypothetically) 100 students in the class, 1 student took the quiz in 3 minutes (180 seconds) so the mean that Canvas calculates is 180/100 or 1.8 seconds. That calculation is actually an average whereas the mean would be the 180 - I am assuming that a quiz not taken is still counted in the sample with a time of 0. Just throwing something out there to see if we can find any semblance of sense out of the calculation. (I think I have the mean and average determined correctly)
Ron
Um, that is one wild quote. It appears you got it from https://www.cuemath.com/data/difference-between-average-and-mean/ ? It's bizarre as it's pretty much saying the same thing twice while falsely alleging it's saying different things.
A mean is a form of an average. So are median, mode, and mid-range. But in common language, mean = average = sum of all items divided by count of items. If Canvas means something other than mean, it needs to change the word it uses.
For quizzes 1-3, all 113 students took it. For quiz 4, 109 students took it. I have a good sample size for all quizzes.
There is no way 113 students took quiz 3, a 19 question quiz, and averaged 3 seconds each. Two of the 113 students had a technical glitch, so I reassigned them an opportunity to retake the quiz. Their grades were fine, so it impossible for them to have warped the mean.
I am still coming up with no rational explanation for what this number is showing me. Even if we say "mean" is mislabeling the number, I am not clear what useful statistic this would possibly be.